从复数的三角形式到欧拉公式——《白话高中数学》复数(五)
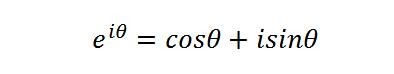
今天聊聊如雷贯耳的欧拉公式,以及德·莫伊夫定理和复数的三角形式之间的关系。
在复平面(也称为阿干特图)上,每一个复数都可以用一个点来表示。
如果这个复数写作z=a+bi,其中a 和 b 是实数,i 是虚数单位(满足i2=−1),那么我们也可以将它转换成极坐标得表达形式:
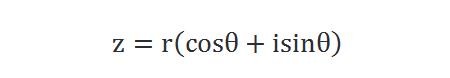
这就是复数的三角形式。其中r为这个复数的绝对值|z|,也就是原点到这个复数点的距离,即复数对应向量的模;θ是复数的幅角,也就是复数的对应向量和x轴正半轴的夹角。
使用三角表达形式给复数的计算带来了巨大的方便:
比如乘除运算方面的简化:当两个复数相乘时,采用三角形式直接模长相乘、幅角相加就行;相除呢,直接模长相除,幅角相减。
也就是这样:
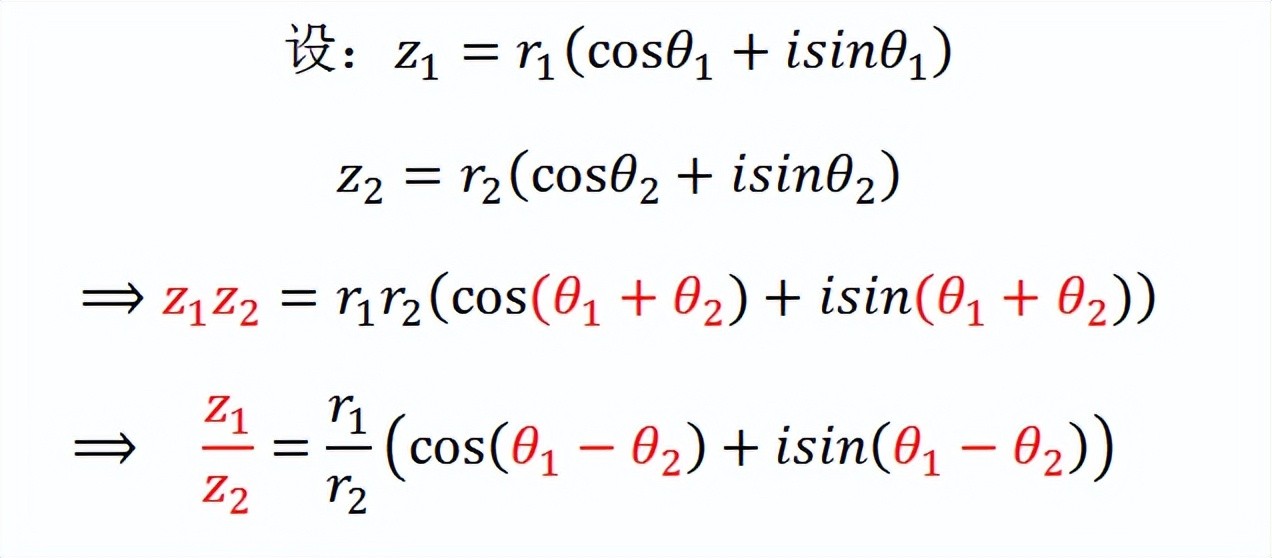
再比如幂和根计算:对于求复数的幂或根,三角形式同样简化了计算过程,比如德·莫伊夫定理(De Moivre's theorem):
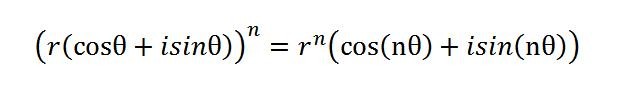
这个定理可以根据n个相同的复数z相乘推导而来,它使得计算复数的幂变得简单,并且还可以用它来求解复数的根,举个例子:
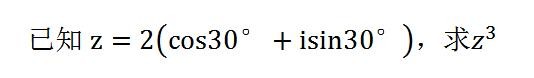
根据定理,直接代入即可:
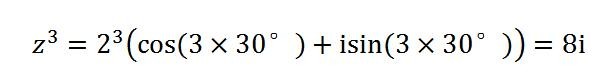
想要对一个复数开根,也会变得非常简单:

我们直接设:
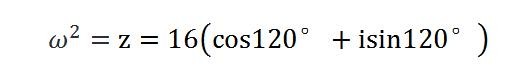
根据定理,上式就可以改写成:
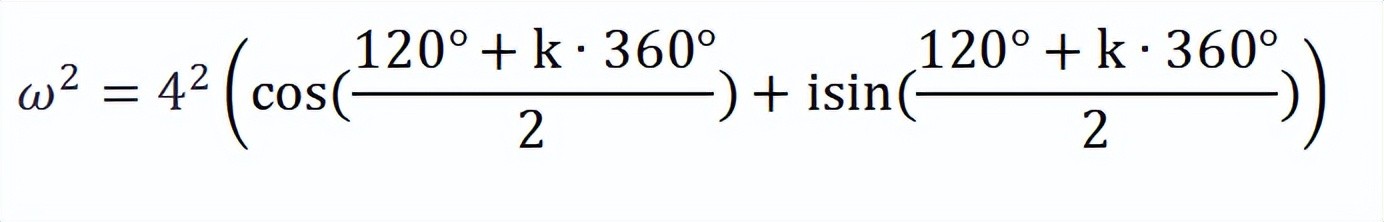
当k=0时:
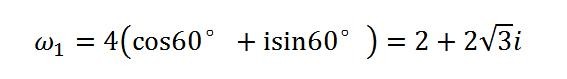
当k=1时:

最有成就感的,就是可以从复数的三角形式推导欧拉公式
欧拉公式是数学中的一个重要恒等式,它建立了复指数函数与三角函数之间的联系,表述为:
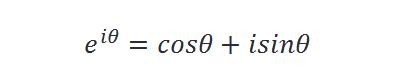
等号左侧是指数形式,右侧是三角函数形式,我们可以从复数的三角表达形式出发,用直观的方式来推导出等号的两边其实是等价的。
首先,如果一个模长为1的复数,幅角是θ,可以写成:
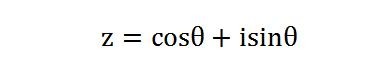
所有符合上式的复数点,在复平面上可以形成一个半径为1的圆。
如果复数z=1刚开始是趴在x轴正半轴上的,给它乘以一个i,就相当于把它旋转了90°,变成了z=i。如果我们拆解上述旋转过程,就会发现这种旋转实际上是通过复数的乘法来完成的:
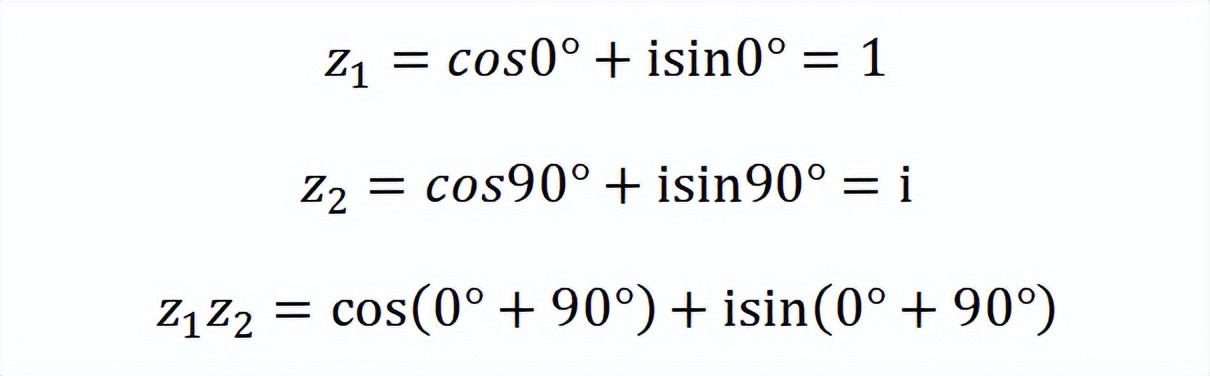
现在,我们给出一个指数函数eθ,首先让θ=0,这就保证了e0=1,
我们把θ限定在一个单位圆里,当乘以一个i,变成iθ时,根据复数乘法的意义,我们任取一个θ,“iθ”就是在“θ”的基础上再旋转90°,模长并没有发生变化,还是r=1。
这就意味着:对于指数函数eiθ来说,任取一个θ值,“iθ”只是进行了旋转操作,那么eiθ也跟着进行了旋转操作,方向不同,但它的|eiθ|没有发生变化,均为1。
同时也就意味着:当θ连续变换时,复指数函数eiθ的轨迹就是复平面上半径为1的圆。
那么,从几何意义上来说,eiθ表示的轨迹和复数cosθ+isinθ表示的轨迹,就是同一个东西,二者是等价的:
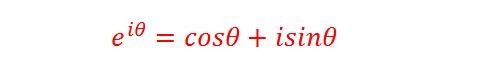
这就是大名鼎鼎的欧拉公式!
它们都是在复平面上,半径为1的单位圆:
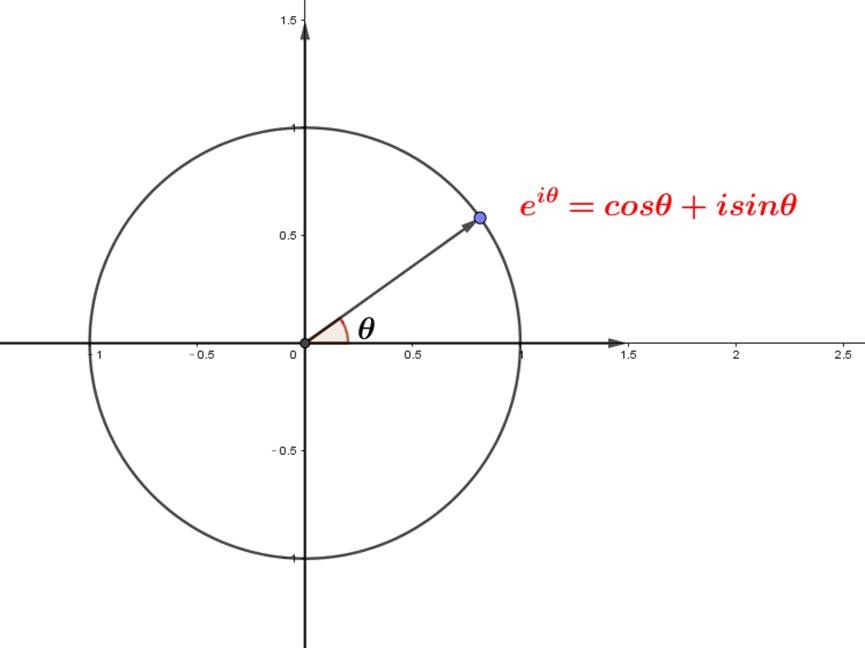
这是从直观上完成欧拉公式的推理,严谨性稍显不足,但好在容易理解。
如果想要严谨地证明欧拉公式,就必须使用泰勒级数展开:
首先是左侧:
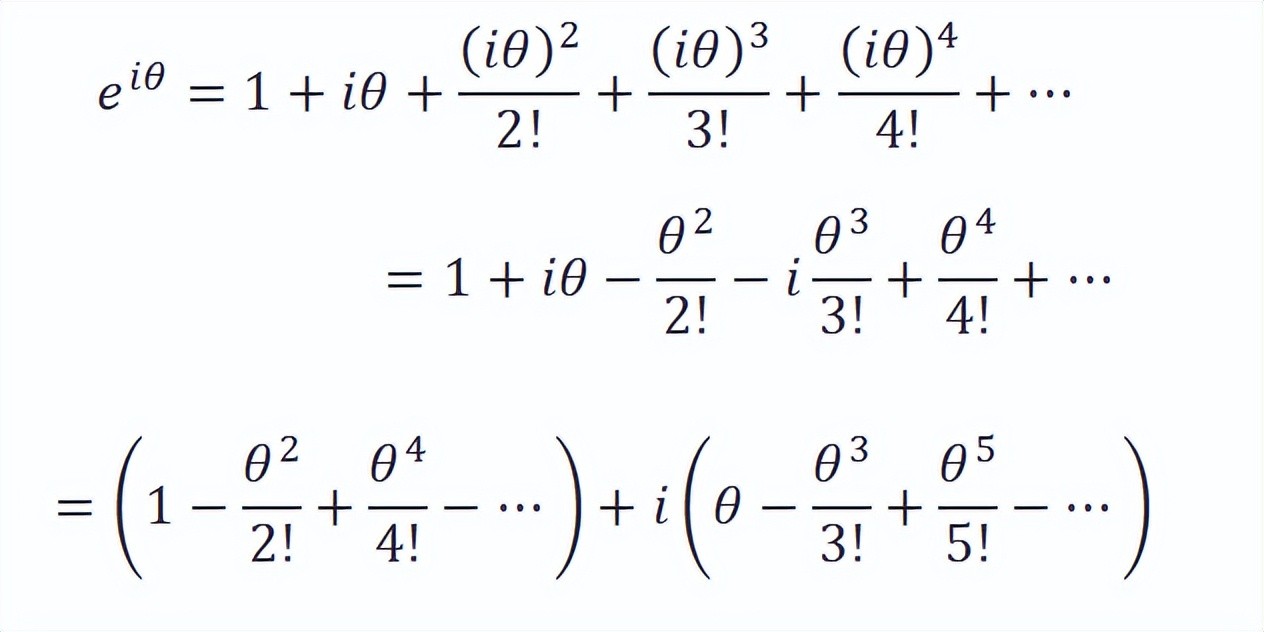
右侧:
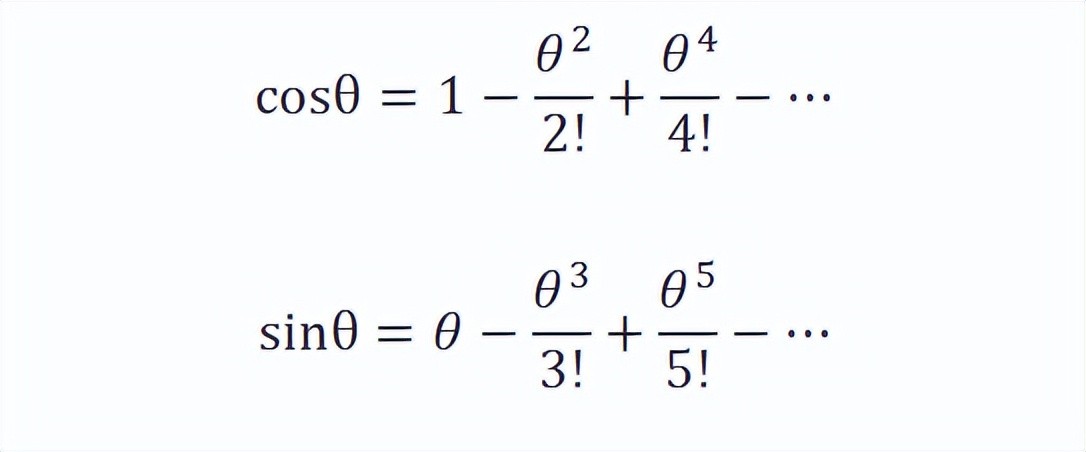
很明显,上式的实部就是cosθ的展开式,虚部就是sinθ的展开式,因此:
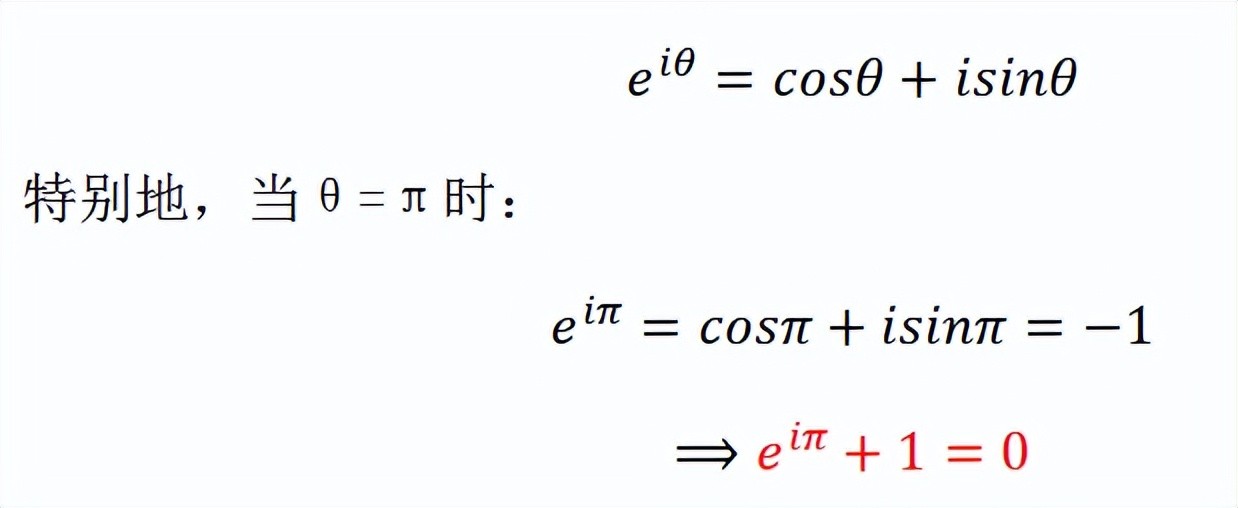
需要原文PDF打印版的,私信就OK!






感谢阅读
